<!DOCTYPE html>
逆推专题什么是逆推法
逆推法,也称为反向推理或逆向思维,是一种从结果出发,通过逐步逆向分析,寻找可能的原因或过程的方法。这种方法在很多领域都有应用,如数学、物理学、逻辑学、甚至日常生活中的问题解决。
逆推法在数学中的应用
在数学中,逆推法常用于解决几何问题、代数方程以及逻辑推理等。例如,在解一个复杂的几何问题时,我们可能首先知道一些边界条件或最终结果,然后通过逆向思考,逐步回溯到问题的起点。这种方法的优点是可以简化问题,减少计算量,并帮助我们更好地理解问题的本质。
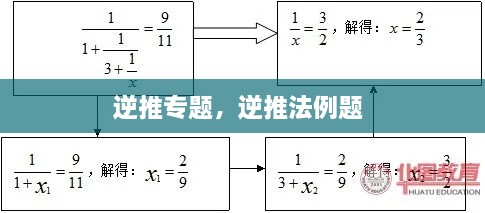
在代数中,逆推法可以用来解方程。比如,我们要解一个二次方程 \(ax^2 + bx + c = 0\),可以先假设一个解 \(x = k\),然后通过将 \(k\) 代入方程,检查它是否满足方程,从而确定 \(k\) 是否为方程的解。这种方法可以快速找到方程的根,尤其是在方程较复杂时。
逆推法在物理学中的应用
在物理学中,逆推法常用于理论分析和实验设计。例如,在研究一个物体的运动轨迹时,我们可以通过测量物体到达终点时的速度和方向,逆向推断出物体在起点时的速度和方向,从而推测出物体可能经历的路径。
在实验设计中,逆推法可以帮助科学家们从预期的结果出发,逆向设计实验步骤,确保实验能够验证理论的正确性。例如,在研究一个化学反应时,科学家们可能首先知道反应的最终产物,然后通过逆向推断出可能的反应物和反应条件,设计实验来验证这些推断。
逆推法在逻辑学中的应用
在逻辑学中,逆推法是证明技巧之一。通过假设结论为真,然后逐步逆向分析,找出支持这个结论的前提,最终证明结论的正确性。这种方法在数学证明和逻辑论证中非常有用。
例如,在证明一个命题时,可以先假设命题的否定为真,然后通过一系列的逻辑推理,最终得出一个矛盾的结论。由此,可以推断出原命题必须为真,因为其否定导致了矛盾。
逆推法在生活中的应用
在生活中,逆推法可以帮助我们解决各种问题。比如,当我们忘记密码时,可以尝试从已知的部分信息逆推可能的密码组合。在寻找失物时,也可以通过记住物品最后出现的地方和时间,逆向推断出可能的丢失路径。
逆推法还适用于决策过程。当我们面临一个决策时,可以先设想决策的结果,然后根据这个结果评估每个选择的利弊,从而做出更明智的选择。
逆推法的局限性
尽管逆推法在很多情况下都非常有效,但它也有其局限性。首先,逆推法依赖于已有的信息,如果信息不准确或不完整,逆推的结果可能会出错。其次,逆推法可能无法解决所有类型的问题,尤其是在需要从多个角度或因素综合分析的问题上。
因此,在实际应用中,逆推法应该与其他方法结合使用,以确保问题的解决更加全面和准确。
结论
逆推法是一种强大的思维工具,可以帮助我们解决各种问题。无论是在数学、物理学、逻辑学还是在日常生活中,逆推法都能够提供一种独特且有效的解决途径。然而,理解和应用逆推法也需要一定的技巧和经验,只有正确地运用它,才能在解决问题的道路上越走越远。
转载请注明来自河南桥梁钢模板厂家_河南高铁模板定制_河南盘扣脚手架租赁_河南铁路模板价格,本文标题:《逆推专题,逆推法例题 》











 蜀ICP备2022005971号-1
蜀ICP备2022005971号-1
还没有评论,来说两句吧...