引言

在几何学中，四边形是一个基本的平面图形，由四条线段组成。特殊四边形是指具有特定性质的四边形，如矩形、菱形、正方形和梯形等。在这些特殊四边形中，动点问题是一个常见的数学问题，它涉及到四边形内或其边界上的点在运动时产生的几何关系。本文将探讨特殊四边形中动点的专题，分析其性质和解决方法。

矩形中的动点

矩形是一种具有四个直角的四边形，其对边相等且平行。在矩形中，一个动点P可以在对角线或边上进行运动。考虑一个矩形ABCD，其中AB和CD是平行边，AD和BC是垂直边。如果点P在AD上运动，那么根据矩形的性质，DP和BC的长度相等。这种性质可以用来解决许多涉及动点P的问题。

菱形中的动点

菱形是一种所有边都相等的四边形，其对角线互相垂直且平分。在菱形中，动点P可以在边或对角线上运动。例如，如果P在对角线AC上，那么根据菱形的性质，AP和PC的长度相等。这种性质在解决动点P与菱形的其他顶点或边的关系问题时非常有用。

正方形中的动点

正方形是一种特殊的矩形和菱形，具有四个相等的边和四个直角。在正方形中，动点P的运动更为简单，因为所有边和角都是相等的。如果P在正方形的一边AB上，那么它可以在AB的任意位置运动，但始终保持与对边CD的对称性。这种对称性在解决与正方形相关的动点问题时提供了便利。

梯形中的动点

梯形是一种只有一对平行边的四边形。在梯形中，动点P可以在平行边或非平行边上运动。如果P在非平行边AD上，那么根据梯形的性质，DP和AB的长度之比等于CD和AB的长度之比。这种比例关系在解决涉及动点P的问题时非常有用。

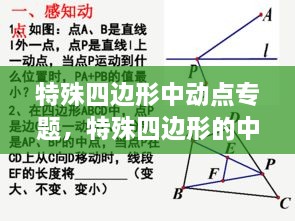
动点与对称性

在特殊四边形中，动点的运动往往与图形的对称性有关。例如，在矩形和正方形中，动点可以在对称轴上运动，而在菱形中，动点可以在对角线上运动。这些对称性可以帮助我们简化问题的解决过程，因为它们提供了额外的几何关系和性质。

动点与几何关系

在解决特殊四边形中动点问题时，理解和应用几何关系至关重要。例如，在矩形中，动点P的轨迹可能是一个圆，而在菱形中，动点P的轨迹可能是一个椭圆。通过分析这些轨迹的几何性质，我们可以找到动点P与四边形其他部分的关系。

动点与轨迹方程

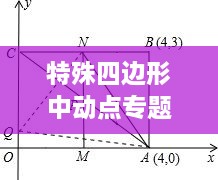
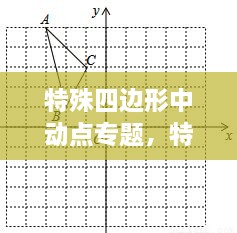
在数学中，动点的轨迹可以用方程来描述。在特殊四边形中，动点P的轨迹方程可能涉及到坐标轴上的坐标，如x和y。通过建立这些方程，我们可以找到动点P的运动规律，并解决与动点相关的几何问题。

结论

特殊四边形中动点专题是一个丰富且有趣的数学领域。通过对矩形、菱形、正方形和梯形等特殊四边形的动点性质和解决方法的研究，我们可以提高对几何图形的理解和应用能力。动点问题不仅考验我们对基本几何概念的理解，还要求我们运用逻辑推理和数学技巧。通过深入探讨这些专题，我们可以更好地掌握几何学的精髓。